อาร์คิมิดีส

2.1. วัยเด็กและการศึกษา

ในงานเขียน The Sand Reckoner อาร์คิมิดีสระบุชื่อบิดาของตนว่า ฟิเดียส ซึ่งเป็นนักดาราศาสตร์ที่ไม่ปรากฏข้อมูลอื่นใดอีก พลูทาร์กเขียนในหนังสือ Parallel Lives ของเขาว่า อาร์คิมิดีสเป็นญาติกับพระเจ้าเฮียโรที่ 2 แห่งซีรากูซา ผู้ปกครองซีรากูซา แม้ว่ากิแกโรจะเสนอว่าเขามีพื้นเพมาจากครอบครัวธรรมดา เพื่อนของอาร์คิมิดีสคนหนึ่งชื่อ เฮราคลีดีส ได้เขียนชีวประวัติของเขา แต่ผลงานนี้สูญหายไป ทำให้รายละเอียดชีวิตของเขายังคงคลุมเครือ เช่น ไม่ทราบว่าเขาแต่งงานหรือมีบุตรหรือไม่ หรือเคยไปเยือนอเล็กซานเดรียในอียิปต์ช่วงวัยเยาว์หรือไม่ จากงานเขียนที่ยังคงหลงเหลืออยู่ของเขา เห็นได้ชัดว่าเขารักษาความสัมพันธ์ฉันมิตรกับนักวิชาการที่นั่น รวมถึงเพื่อนของเขาอย่างโคนอนแห่งซามอส และบรรณารักษ์ใหญ่เอราทอสเทนีสแห่งไซรีน ในบทนำของ On Spirals ที่ส่งถึงโดซิเธอุสแห่งเพลูเซียม อาร์คิมิดีสกล่าวว่า "หลายปีได้ผ่านพ้นไปนับตั้งแต่โคนอนเสียชีวิต" ซึ่งโคนอนแห่งซามอสมีชีวิตอยู่ระหว่างประมาณ 280-220 ปีก่อนคริสตกาล บ่งชี้ว่าอาร์คิมิดีสอาจเป็นผู้สูงอายุแล้วเมื่อเขียนผลงานบางชิ้นของเขา

2.2. การทำงาน

บันทึกมาตรฐานเกี่ยวกับชีวิตของอาร์คิมิดีสถูกเขียนขึ้นหลังจากที่เขาเสียชีวิตไปนานแล้วโดยนักประวัติศาสตร์กรีกและโรมัน การกล่าวถึงอาร์คิมิดีสครั้งแรกปรากฏใน Histories ของพอลิเบียส (ประมาณ 200-118 ปีก่อนคริสตกาล) ซึ่งเขียนขึ้นประมาณ 70 ปีหลังจากการเสียชีวิตของเขา บันทึกนี้ให้ข้อมูลเกี่ยวกับอาร์คิมิดีสในฐานะบุคคลเพียงเล็กน้อย และเน้นไปที่เครื่องจักรสงครามที่เขาถูกกล่าวขานว่าสร้างขึ้นเพื่อปกป้องเมืองจากชาวโรมัน พอลิเบียสกล่าวถึงว่า ในช่วงสงครามพิวนิกครั้งที่สอง ซีรากูซาได้เปลี่ยนข้างจากสาธารณรัฐโรมันไปเข้ากับคาร์เธจ ส่งผลให้เกิดการรณรงค์ทางทหารภายใต้การบัญชาการของมาร์กุส เกลาดิอุส มาร์แก็ลลุส และอัปปิอุส เกลาดิอุส ปุลเคร์ ผู้ซึ่งปิดล้อมเมืองตั้งแต่ 213 ถึง 212 ปีก่อนคริสตกาล เขาบันทึกว่าชาวโรมันประเมินการป้องกันของซีรากูซาต่ำไป และกล่าวถึงเครื่องจักรหลายชิ้นที่อาร์คิมิดีสออกแบบ รวมถึงเครื่องยิงหินที่ได้รับการปรับปรุง เครื่องจักรคล้ายเครนที่สามารถเหวี่ยงเป็นวงโค้งได้ และเครื่องขว้างก้อนหินอื่นๆ แม้ชาวโรมันจะยึดเมืองได้ในที่สุด แต่พวกเขาก็ได้รับความสูญเสียอย่างมากจากความอัจฉริยะของอาร์คิมิดีส

กิแกโร (106-43 ปีก่อนคริสตกาล) กล่าวถึงอาร์คิมิดีสในงานเขียนบางชิ้นของเขา ขณะดำรงตำแหน่งขุนคลังในซิซิลี กิแกโรพบสิ่งที่สันนิษฐานว่าเป็นหลุมศพของอาร์คิมิดีสใกล้ประตูอกริเจจนทีนในซีรากูซา ซึ่งอยู่ในสภาพถูกทอดทิ้งและปกคลุมไปด้วยพุ่มไม้ กิแกโรสั่งให้ทำความสะอาดหลุมศพและสามารถมองเห็นภาพแกะสลักและอ่านบทกวีบางส่วนที่ถูกเพิ่มเป็นจารึกได้ หลุมศพมีรูปปั้นที่แสดงถึงการพิสูจน์ทางคณิตศาสตร์ที่อาร์คิมิดีสชื่นชอบ นั่นคือปริมาตรและพื้นที่ผิวของทรงกลมเป็นสองในสามของทรงกระบอกที่บรรจุอยู่ รวมถึงฐานของทรงกระบอกด้วย เขายังกล่าวถึงว่ามาร์เซลลัสนำท้องฟ้าจำลองสองเครื่องที่อาร์คิมิดีสสร้างขึ้นกลับไปยังโรม นักประวัติศาสตร์โรมันลิวี (59 ปีก่อนคริสตกาล-17 ปีหลังคริสตกาล) เล่าเรื่องราวของพอลิเบียสเกี่ยวกับการยึดซีรากูซาและบทบาทของอาร์คิมิดีสในการนั้น

2.3. การเสียชีวิต

พลูทาร์ก (45-119 ปีหลังคริสตกาล) ให้เรื่องราวอย่างน้อยสองเรื่องเกี่ยวกับวิธีที่อาร์คิมิดีสเสียชีวิตหลังจากซีรากูซาถูกยึด ตามเรื่องราวที่เป็นที่นิยมที่สุด อาร์คิมิดีสกำลังครุ่นคิดถึงแผนภาพทางคณิตศาสตร์เมื่อเมืองถูกยึด ทหารโรมันคนหนึ่งสั่งให้เขามาพบมาร์เซลลัส แต่เขาปฏิเสธโดยกล่าวว่าเขาต้องทำงานแก้ปัญหาให้เสร็จ สิ่งนี้ทำให้ทหารโกรธจัด และเขาได้สังหารอาร์คิมิดีสด้วยดาบของเขา อีกเรื่องหนึ่งเล่าว่าอาร์คิมิดีสกำลังถือเครื่องมือทางคณิตศาสตร์ก่อนที่จะถูกสังหาร เพราะทหารคิดว่ามันเป็นของมีค่า มาร์เซลลัสถูกกล่าวขานว่าโกรธมากกับการเสียชีวิตของอาร์คิมิดีส เนื่องจากเขาถือว่าอาร์คิมิดีสเป็นทรัพย์สินทางวิทยาศาสตร์ที่มีคุณค่า (เขาเรียกอาร์คิมิดีสว่า "ไบรอาเรอุสทางเรขาคณิต") และได้ออกคำสั่งว่าไม่ควรทำอันตรายเขา

คำพูดสุดท้ายที่เชื่อกันว่าอาร์คิมิดีสกล่าวคือ "อย่ากวนวงกลมของข้า" (Noli turbare circulos meos^{ภาษาละติน}; μὴ μου τοὺς κύκลους τάραττε^{ภาษากรีก (ใหม่)}) ซึ่งอ้างถึงภาพวาดทางคณิตศาสตร์ที่เขาถูกกล่าวหาว่ากำลังศึกษาอยู่เมื่อถูกทหารโรมันรบกวน ไม่มีหลักฐานที่น่าเชื่อถือว่าอาร์คิมิดีสกล่าวคำเหล่านี้จริง และไม่ปรากฏในบันทึกของพลูทาร์ก คำกล่าวที่คล้ายกันพบในงานของวาเลริอุส มักซิมุส (ประมาณ 30 ปีหลังคริสตกาล) ผู้เขียนใน Memorable Doings and Sayings ว่า "... sed protecto manibus puluere 'noli' inquit, 'obsecro, istum disturbare'^{ภาษาละติน}" ("... แต่ปกป้องฝุ่นด้วยมือของเขา กล่าวว่า 'ข้าขอร้อง อย่ารบกวนสิ่งนี้'")

3.1. วิธีการเกษียณและอนันต์

อาร์คิมิดีสสามารถใช้แนวคิดของกณิกนันต์ (ซึ่งเป็นแนวคิดตั้งต้นของอนันต์) ในลักษณะที่คล้ายคลึงกับแคลคูลัสเชิงปริพันธ์สมัยใหม่ ด้วยการพิสูจน์โดยการแย้ง (reductio ad absurdum) เขาสามารถให้คำตอบสำหรับปัญหาต่างๆ ได้ในระดับความแม่นยำที่กำหนดเองได้ พร้อมทั้งระบุขีดจำกัดที่คำตอบนั้นอยู่ เทคนิคนี้รู้จักกันในชื่อระเบียบวิธีเกษียณ และเขาใช้มันเพื่อประมาณพื้นที่ของรูปทรงและค่าπ

3.2. การคำนวณค่าพาย

ในงานเขียน Measurement of a Circle เขาทำได้โดยการวาดรูปหกเหลี่ยมปกติขนาดใหญ่กว่าอยู่นอกวงกลม จากนั้นวาดรูปหกเหลี่ยมปกติขนาดเล็กกว่าอยู่ภายในวงกลม และค่อยๆ เพิ่มจำนวนด้านของรูปหลายเหลี่ยมปกติแต่ละรูปเป็นสองเท่า โดยคำนวณความยาวของด้านแต่ละรูปในแต่ละขั้นตอน เมื่อจำนวนด้านเพิ่มขึ้น รูปหลายเหลี่ยมก็จะใกล้เคียงกับวงกลมมากขึ้น หลังจากสี่ขั้นตอนดังกล่าว เมื่อรูปหลายเหลี่ยมแต่ละรูปมี 96 ด้าน เขาสามารถกำหนดได้ว่าค่าของ π อยู่ระหว่าง 3 1/7 (ประมาณ 3.1429) และ 3 10/71 (ประมาณ 3.1408) ซึ่งสอดคล้องกับค่าจริงของมันที่ประมาณ 3.1416 เขายังพิสูจน์ด้วยว่าพื้นที่ของวงกลมเท่ากับ π คูณกับกำลังสองของรัศมีของวงกลม

3.3. เรขาคณิต

ในงานเขียน Quadrature of the Parabola อาร์คิมิดีสพิสูจน์ว่าพื้นที่ที่ถูกปิดล้อมด้วยพาราโบลาและเส้นตรงมีค่าเป็น 4/3 เท่าของพื้นที่สามเหลี่ยมที่อยู่ภายในที่สอดคล้องกัน ดังแสดงในรูปด้านขวา เขาแสดงผลลัพธ์ของปัญหานี้เป็นอนุกรมเรขาคณิตอนันต์ที่มีอัตราส่วนร่วม 1/4:
1 + 4^-1 + 4^-2 + 4^-3 + ... = 4/3
หากพจน์แรกในอนุกรมนี้คือพื้นที่ของสามเหลี่ยม พจน์ที่สองคือผลรวมของพื้นที่ของสามเหลี่ยมสองรูปที่มีฐานเป็นเส้นตัดที่เล็กกว่าสองเส้น และจุดยอดที่สามคือจุดที่เส้นขนานกับแกนของพาราโบลาและผ่านจุดกึ่งกลางของฐานตัดกับพาราโบลา และเป็นเช่นนี้ไปเรื่อยๆ การพิสูจน์นี้ใช้การแปรผันของอนุกรม 1/4 + 1/16 + 1/64 + 1/256 + · · · ซึ่งมีผลรวมเป็น 1/3

3.4. คุณสมบัติของอาร์คิมิดีส

ในงานเขียน On the Sphere and Cylinder อาร์คิมิดีสตั้งสมมติฐานว่าปริมาณใดๆ เมื่อนำมาบวกกับตัวเองมากพอ จะเกินกว่าปริมาณใดๆ ที่กำหนดให้ วันนี้สิ่งนี้รู้จักกันในชื่อคุณสมบัติแบบอาร์คิมิดีสของจำนวนจริง

ใน Measurement of a Circle อาร์คิมิดีสให้ค่ารากที่สองของ 3 ว่าอยู่ระหว่าง 265/153 (ประมาณ 1.7320261) และ 1351/780 (ประมาณ 1.7320512) โดยค่าจริงคือประมาณ 1.7320508 ซึ่งเป็นการประมาณที่แม่นยำมาก เขาเสนอผลลัพธ์นี้โดยไม่ได้ให้คำอธิบายว่าเขาได้มาได้อย่างไร แง่มุมนี้ของผลงานของอาร์คิมิดีสทำให้จอห์น วอลลิสกล่าวว่าเขา: "ราวกับว่าตั้งใจที่จะปกปิดร่องรอยของการสอบสวนของเขา ราวกับว่าเขาอิจฉาคนรุ่นหลังในความลับของวิธีการสอบสวนของเขา ในขณะที่เขาต้องการบังคับให้พวกเขายอมรับผลลัพธ์ของเขา" เป็นไปได้ว่าเขาใช้วิธีการวนซ้ำเพื่อคำนวณค่าเหล่านี้

3.5. การนับเม็ดทราย

ในงานเขียน The Sand Reckoner อาร์คิมิดีสตั้งใจที่จะคำนวณจำนวนที่มากกว่าจำนวนเม็ดทรายที่จำเป็นในการเติมจักรวาลทั้งหมด การทำเช่นนั้น เขาได้ท้าทายแนวคิดที่ว่าจำนวนเม็ดทรายนั้นใหญ่เกินกว่าจะนับได้ เขาเขียนว่า:
"มีบางคน พระเจ้าเจโล ผู้คิดว่าจำนวนเม็ดทรายนั้นมีมากมายจนเป็นอนันต์ และข้ามิได้หมายถึงทรายที่มีอยู่ในซีรากูซาและส่วนที่เหลือของซิซิลีเท่านั้น แต่รวมถึงทรายที่พบในทุกภูมิภาคไม่ว่าจะมีคนอาศัยอยู่หรือไม่ก็ตาม"
เพื่อแก้ปัญหานี้ อาร์คิมิดีสได้คิดค้นระบบการนับที่อิงจากมีเรียด คำนี้มาจากภาษากรีก μυριάς^{Greek, Ancient} ซึ่งหมายถึงจำนวน 10,000 เขาเสนอระบบจำนวนโดยใช้กำลังของมีเรียดของมีเรียด (100 ล้าน หรือ 10,000 x 10,000) และสรุปว่าจำนวนเม็ดทรายที่จำเป็นในการเติมจักรวาลทั้งหมดคือ 8 x 10⁶³

3.6. งานเขียนหลัก (คณิตศาสตร์)

ผลงานทางคณิตศาสตร์หลักของอาร์คิมิดีสที่ยังคงอยู่ ได้แก่ ว่าด้วยการวัดวงกลม, การหาพื้นที่ของพาราโบลา, ว่าด้วยทรงกลมและทรงกระบอก, ว่าด้วยเส้นเกลียว, ว่าด้วยทรงกรวยและทรงกลม, ว่าด้วยเทหวัตถุลอย, โอสโตมาคิออน, ปัญหาเรื่องวัวของอาร์คิมิดีส, นักคำนวณทราย และ ระเบียบวิธีเกี่ยวกับทฤษฎีบทกลศาสตร์

4.1. หลักการของแรงลอยตัว

เรื่องเล่าที่รู้จักกันแพร่หลายที่สุดเกี่ยวกับอาร์คิมิดีสคือการที่เขาคิดค้นวิธีหาปริมาตรของวัตถุที่มีรูปร่างไม่สม่ำเสมอ ตามบันทึกของวิทรูเวียส พระเจ้าเฮียโรที่ 2 แห่งซีรากูซาทรงสั่งให้ทำมงกุฎสำหรับวัด โดยทรงจัดหาทองคำบริสุทธิ์ให้ อาร์คิมิดีสได้รับมอบหมายให้ตรวจสอบว่าช่างทองได้นำเงินมาผสมแทนทองคำบางส่วนหรือไม่โดยไม่ทำลายมงกุฎ ดังนั้นเขาจึงไม่สามารถหลอมมันให้เป็นรูปทรงปกติเพื่อคำนวณความหนาแน่นได้

ในเรื่องเล่านี้ อาร์คิมิดีสสังเกตขณะอาบน้ำว่าระดับน้ำในอ่างสูงขึ้นเมื่อเขาลงไป และตระหนักว่าผลกระทบนี้สามารถใช้เพื่อกำหนดปริมาตรของมงกุฎทองคำได้ เพื่อวัตถุประสงค์ในทางปฏิบัติ น้ำไม่สามารถบีบอัดได้ ดังนั้นมงกุฎที่จมลงไปจะแทนที่น้ำในปริมาณที่เท่ากับปริมาตรของมันเอง โดยการนำมวลของมงกุฎหารด้วยปริมาตรของน้ำที่ถูกแทนที่ จะสามารถหาความหนาแน่นของมันได้ หากมีการเพิ่มโลหะที่ราคาถูกกว่าและมีความหนาแน่นน้อยกว่า ความหนาแน่นก็จะต่ำกว่าทองคำ อาร์คิมิดีสพบว่านี่คือสิ่งที่เกิดขึ้น ซึ่งพิสูจน์ว่ามีการผสมเงินเข้าไป อาร์คิมิดีสรู้สึกตื่นเต้นกับการค้นพบนี้มากจนวิ่งออกไปตามถนนทั้งที่ยังเปลือยกาย ลืมแต่งตัว และร้องตะโกนว่า "ยูเรก้า!" (εὕρηκα!^{ภาษากรีก (ใหม่)}, heúrēka!, แปลว่า ฉันพบแล้ว!)

เรื่องราวของมงกุฎทองคำไม่ปรากฏในผลงานที่รู้จักของอาร์คิมิดีส ความเป็นไปได้ในทางปฏิบัติของวิธีการที่อธิบายไว้ถูกตั้งคำถามเนื่องจากความแม่นยำอย่างยิ่งยวดที่จำเป็นในการวัดการแทนที่ของน้ำ อาร์คิมิดีสอาจแสวงหาวิธีแก้ปัญหาที่ประยุกต์ใช้หลักการอุทกสถิตศาสตร์ที่รู้จักกันในชื่อหลักการของอาร์คิมิดีส ซึ่งพบในตำราของเขาเรื่อง On Floating Bodies: วัตถุที่จมอยู่ในของไหลจะประสบกับแรงลอยตัวเท่ากับน้ำหนักของของไหลที่มันแทนที่ ด้วยหลักการนี้ เป็นไปได้ที่จะเปรียบเทียบความหนาแน่นของมงกุฎกับทองคำบริสุทธิ์โดยการถ่วงบนเครื่องชั่งกับตัวอย่างทองคำบริสุทธิ์ที่มีน้ำหนักเท่ากัน จากนั้นจุ่มอุปกรณ์ลงในน้ำ ความแตกต่างของความหนาแน่นระหว่างสองตัวอย่างจะทำให้เครื่องชั่งเอียงตามนั้น กาลิเลโอ กาลิเลอี ผู้คิดค้นสมดุลสถิตยศาสตร์ของไหลในปี ค.ศ. 1586 โดยได้รับแรงบันดาลใจจากงานของอาร์คิมิดีส พิจารณาว่า "เป็นไปได้ว่าวิธีนี้เป็นวิธีเดียวกับที่อาร์คิมิดีสใช้ เนื่องจากนอกจากจะแม่นยำมากแล้ว ยังอิงจากการสาธิตที่อาร์คิมิดีสเองได้ค้นพบ"

4.2. กฎของคาน

แม้ว่าอาร์คิมิดีสจะไม่ได้เป็นผู้ประดิษฐ์คาน แต่เขาได้ให้การพิสูจน์ทางคณิตศาสตร์ของหลักการที่เกี่ยวข้องในงานเขียนของเขาเรื่อง On the Equilibrium of Planes คำอธิบายก่อนหน้านี้เกี่ยวกับหลักการของคานพบในงานของยูคลิดและใน Mechanical Problems ซึ่งเป็นของสำนักศึกษาเพริพาเททิก ซึ่งเป็นผู้ติดตามของอริสโตเติล การประพันธ์ซึ่งบางคนเชื่อว่าเป็นของอาร์คีตัส

มีรายงานหลายฉบับ ซึ่งมักจะขัดแย้งกัน เกี่ยวกับความสามารถของอาร์คิมิดีสในการใช้คานเพื่อยกวัตถุที่หนักมาก พลูทาร์กบรรยายถึงวิธีที่อาร์คิมิดีสออกแบบระบบรอกทดกำลัง ซึ่งช่วยให้ลูกเรือสามารถใช้หลักการของคานเพื่อยกวัตถุที่ปกติแล้วหนักเกินกว่าจะเคลื่อนย้ายได้ ตามบันทึกของพัพพัสแห่งอเล็กซานเดรีย งานของอาร์คิมิดีสเกี่ยวกับคานและความเข้าใจของเขาเกี่ยวกับความได้เปรียบทางกลทำให้เขากล่าวว่า: "หาที่ยืนให้ฉันสิ แล้วฉันจะเคลื่อนโลกให้" (δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κินάσω_{ดอซ มอย ปา สโต ไค ตาน กาน คินาโซ}^{ภาษากรีก (ใหม่)}) โอลิมปิโอโดรุสผู้เยาว์ในภายหลังได้กล่าวอ้างคำพูดเดียวกันนี้กับสิ่งประดิษฐ์ของอาร์คิมิดีสที่เรียกว่า บารูลคอส ซึ่งเป็นเครื่องกว้านชนิดหนึ่ง มากกว่าจะเป็นคาน

4.3. สถิตยศาสตร์และอุทกสถิตศาสตร์

อาร์คิมิดีสมีส่วนร่วมอย่างกว้างขวางในสาขาสถิตยศาสตร์และอุทกสถิตศาสตร์ รวมถึงแนวคิดเรื่องจุดศูนย์กลางมวล ในงานเขียน On Floating Bodies เขาได้อธิบายกฎของสมดุลของของไหลและพิสูจน์ว่าน้ำจะคงรูปทรงเป็นทรงกลมรอบจุดศูนย์กลางของแรงโน้มถ่วง ซึ่งอาจเป็นความพยายามที่จะอธิบายทฤษฎีของนักดาราศาสตร์กรีกร่วมสมัย เช่น เอราทอสเทนีส ที่ว่าโลกมีรูปร่างกลม ของไหลที่อาร์คิมิดีสบรรยายนั้นไม่ได้มีแรงโน้มถ่วงในตัวเอง เนื่องจากเขาสมมติฐานว่ามีจุดหนึ่งที่ทุกสิ่งตกลงไปหาเพื่อที่จะได้รูปทรงกลม

4.4. สิ่งประดิษฐ์

อาร์คิมิดีสได้ออกแบบสิ่งประดิษฐ์และกลไกต่างๆ ที่แสดงถึงความอัจฉริยะทางวิศวกรรมของเขา หลายสิ่งประดิษฐ์เหล่านี้ถูกนำไปใช้เพื่อตอบสนองความต้องการของเมืองซีรากูซาและเพื่อวัตถุประสงค์ทางทหาร

4.4.1. เครื่องสูบแบบเกลียว (Vít Archimedes / Archimedes' screw)

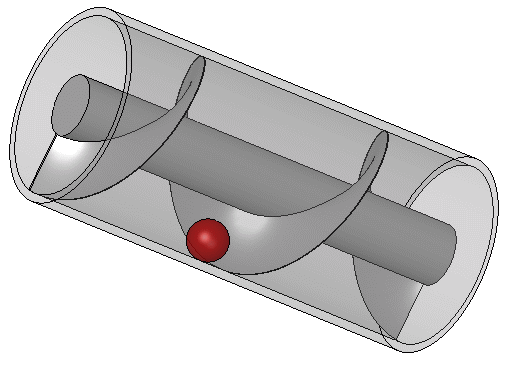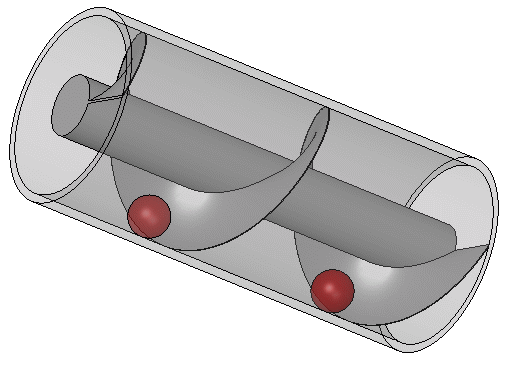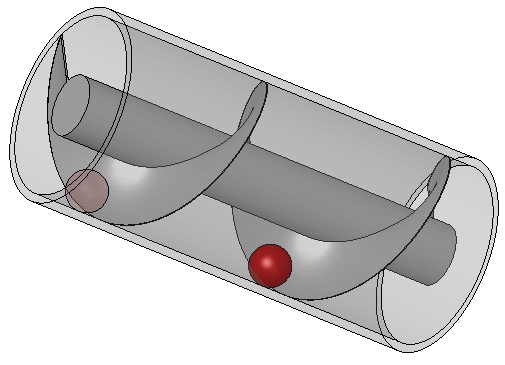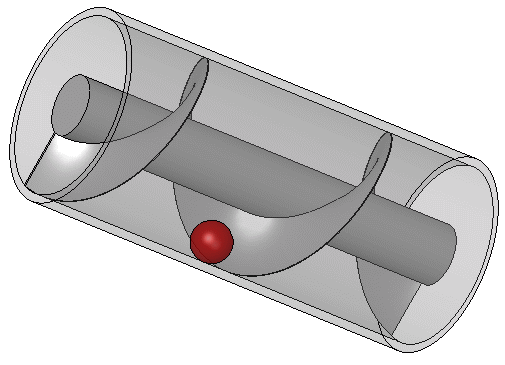
งานส่วนใหญ่ของอาร์คิมิดีสทางด้านวิศวกรรมน่าจะเกิดจากการตอบสนองความต้องการของบ้านเกิดของเขาคือเมืองซีรากูซา อะธีเนอุสแห่งเนาเครติสอ้างถึงมอสคิออนในคำบรรยายว่าพระเจ้าเฮียโรที่ 2 แห่งซีรากูซาทรงสั่งให้อาร์คิมิดีสออกแบบเรือขนาดยักษ์ชื่อ ไซราคูเซีย ซึ่งสามารถใช้สำหรับการเดินทางที่หรูหรา การขนส่งเสบียง และเป็นเครื่องแสดงอำนาจทางทะเล เรือไซราคูเซียถูกกล่าวขานว่าเป็นเรือที่ใหญ่ที่สุดที่สร้างขึ้นในสมัยคลาสสิก และตามบันทึกของมอสคิออน อาร์คิมิดีสเป็นผู้ปล่อยเรือลงน้ำ เรือลำนี้เชื่อกันว่าสามารถบรรทุกคนได้ 600 คน และมีสิ่งอำนวยความสะดวกต่างๆ เช่น สวน ห้องยิมเนเซียม และวิหารที่อุทิศแด่เทพีอโฟรไดท์ บันทึกยังกล่าวถึงว่า เพื่อกำจัดน้ำที่อาจรั่วซึมผ่านตัวเรือ อาร์คิมิดีสได้ออกแบบอุปกรณ์ที่มีใบพัดรูปเกลียวหมุนอยู่ภายในทรงกระบอก

เครื่องสูบแบบเกลียวของอาร์คิมิดีสถูกหมุนด้วยมือ และยังสามารถใช้ในการถ่ายโอนน้ำจากแหล่งน้ำที่ต่ำไปยังคลองชลประทานได้ ปัจจุบันเกลียวนี้ยังคงใช้ในการสูบของเหลวและของแข็งที่เป็นเม็ด เช่น ถ่านหินและเมล็ดพืช ตามที่วิทรูเวียสบรรยายไว้ อุปกรณ์ของอาร์คิมิดีสอาจเป็นการปรับปรุงปั๊มเกลียวที่ใช้ในการชลประทานสวนลอยแห่งบาบิโลน เรือไอน้ำลำแรกของโลกที่มีใบจักรแบบเกลียวคือ SS Archimedes ซึ่งเปิดตัวในปี ค.ศ. 1839 และตั้งชื่อเพื่อเป็นเกียรติแก่อาร์คิมิดีสและผลงานของเขาเกี่ยวกับเกลียว

4.4.2. เครื่องจักรสงคราม

อาร์คิมิดีสถูกกล่าวขานว่าได้ออกแบบกรงเล็บของอาร์คิมิดีสเพื่อเป็นอาวุธป้องกันเมืองซีรากูซา หรือที่รู้จักกันในชื่อ "เครื่องเขย่าเรือ" กรงเล็บประกอบด้วยแขนคล้ายเครนซึ่งมีขอเกี่ยวโลหะขนาดใหญ่แขวนอยู่ เมื่อกรงเล็บถูกปล่อยลงบนเรือที่โจมตี แขนจะเหวี่ยงขึ้น ยกเรือขึ้นจากน้ำและอาจทำให้เรือจม มีการทดลองสมัยใหม่เพื่อทดสอบความเป็นไปได้ของกรงเล็บ และในปี ค.ศ. 2005 สารคดีโทรทัศน์เรื่อง Superweapons of the Ancient World ได้สร้างกรงเล็บขึ้นมาและสรุปว่ามันเป็นอุปกรณ์ที่ใช้งานได้จริง

อาร์คิมิดีสยังได้รับเครดิตในการปรับปรุงพลังและความแม่นยำของเครื่องยิงหิน และในการประดิษฐ์มาตรวัดระยะทาง (odometer) ในช่วงสงครามพิวนิกครั้งที่หนึ่ง มาตรวัดระยะทางถูกบรรยายว่าเป็นรถเข็นที่มีกลไกฟันเฟืองที่ปล่อยลูกบอลลงในภาชนะหลังจากเดินทางไปได้ทุกหนึ่งไมล์

4.4.4. สิ่งประดิษฐ์อื่น ๆ

ตามตำนานเล่าว่า อาร์คิมิดีสจัดเรียงกระจกเป็นจานสะท้อนแบบพาราโบลาเพื่อเผาเรือที่โจมตีซีรากูซาโดยใช้แสงอาทิตย์ที่รวมแสง แม้ว่าจะไม่มีหลักฐานร่วมสมัยที่ยังคงอยู่ของความสำเร็จนี้ และนักวิชาการสมัยใหม่เชื่อว่าสิ่งนี้ไม่ได้เกิดขึ้น แต่อาร์คิมิดีสอาจเขียนงานเกี่ยวกับกระจกชื่อ Catoptrica และลูเชียนกับกาเลน ซึ่งเขียนในคริสต์ศตวรรษที่ 2 กล่าวถึงว่าระหว่างการล้อมซีรากูซา (214-212 ปีก่อนคริสตกาล) อาร์คิมิดีสได้เผาเรือศัตรู เกือบสี่ร้อยปีต่อมา แอนธีมิอุสแห่งทรอลเลส แม้จะสงสัย แต่ก็พยายามสร้างเรขาคณิตของกระจกสะท้อนแสงสมมุติของอาร์คิมิดีสขึ้นมาใหม่

อุปกรณ์ที่ถูกกล่าวอ้างนี้ บางครั้งเรียกว่า "รังสีความร้อนของอาร์คิมิดีส" เป็นหัวข้อของการถกเถียงอย่างต่อเนื่องเกี่ยวกับความน่าเชื่อถือของมันตั้งแต่ยุคฟื้นฟูศิลปวิทยา เรอเน เดส์คาร์ตส์ปฏิเสธว่าไม่เป็นความจริง ในขณะที่นักวิจัยสมัยใหม่พยายามสร้างผลกระทบนี้ขึ้นมาใหม่โดยใช้เพียงวิธีการที่อาร์คิมิดีสมีอยู่ในยุคนั้น ซึ่งส่วนใหญ่ให้ผลลัพธ์เชิงลบ มีการเสนอว่าแผงสำริดหรือทองแดงที่ขัดมันจำนวนมากที่ทำหน้าที่เป็นกระจกอาจถูกนำมาใช้เพื่อรวมแสงอาทิตย์ไปยังเรือ แต่ผลกระทบโดยรวมจะทำให้ลูกเรือของเรือตาพร่ามัว สว่างจ้า หรือทำให้เสียสมาธิมากกว่าที่จะทำให้เกิดเพลิงไหม้ การใช้วัสดุสมัยใหม่และขนาดที่ใหญ่ขึ้น เตารังสีแสงอาทิตย์ที่รวมแสงอาทิตย์สามารถเข้าถึงอุณหภูมิที่สูงมาก และบางครั้งก็ใช้ในการผลิตไฟฟ้า

5.1. งานที่ยังหลงเหลืออยู่

ต่อไปนี้เรียงตามลำดับเวลาตามเกณฑ์ทางศัพท์และประวัติศาสตร์ใหม่ที่กำหนดโดย Knorr (1978) และ Sato (1986)

• ว่าด้วยการวัดวงกลม

เป็นงานสั้นๆ ประกอบด้วยสามบท เขียนในรูปแบบการสนทนากับโดซิเธอุสแห่งเพลูเซียม ผู้เป็นศิษย์ของโคนอนแห่งซามอส ในบทที่สอง อาร์คิมิดีสให้ค่าประมาณของπ โดยแสดงว่ามันมีค่ามากกว่า 223/71 (3.1408...) และน้อยกว่า 22/7 (3.1428...)

• นักคำนวณทราย

ในตำรานี้ หรือที่รู้จักกันในชื่อ Psammites อาร์คิมิดีสได้พบจำนวนที่มากกว่าจำนวนเม็ดทรายที่จำเป็นในการเติมจักรวาลทั้งหมด หนังสือเล่มนี้กล่าวถึงทฤษฎีดวงอาทิตย์เป็นศูนย์กลางของระบบสุริยะที่เสนอโดยอริสทาร์คัสแห่งซามอส รวมถึงแนวคิดร่วมสมัยเกี่ยวกับขนาดของโลกและระยะห่างระหว่างเทหวัตถุต่างๆ และพยายามวัดเส้นผ่านศูนย์กลางปรากฏของดวงอาทิตย์ โดยใช้ระบบตัวเลขที่อิงตามกำลังของมีเรียด อาร์คิมิดีสสรุปว่าจำนวนเม็ดทรายที่จำเป็นในการเติมจักรวาลคือ 8 x 10⁶³ ในสัญกรณ์สมัยใหม่ จดหมายนำเรื่องระบุว่าบิดาของอาร์คิมิดีสเป็นนักดาราศาสตร์ชื่อฟิเดียส The Sand Reckoner เป็นงานเขียนที่ยังคงเหลือรอดเพียงชิ้นเดียวที่อาร์คิมิดีสกล่าวถึงมุมมองของเขาเกี่ยวกับดาราศาสตร์

• ว่าด้วยดุลยภาพของระนาบ

มีสองเล่มใน On the Equilibrium of Planes: เล่มแรกมีสัจพจน์เจ็ดข้อและบทตั้งสิบห้าข้อ ในขณะที่เล่มที่สองมีสิบบทตั้ง ในเล่มแรก อาร์คิมิดีสพิสูจน์กฎของคาน ซึ่งระบุว่า:
"ขนาดอยู่ในสมดุลที่ระยะห่างผกผันกับน้ำหนัก"
อาร์คิมิดีสใช้หลักการที่ได้มาเพื่อคำนวณพื้นที่และจุดศูนย์กลางมวลของรูปทรงเรขาคณิตต่างๆ รวมถึงสามเหลี่ยม สี่เหลี่ยมด้านขนาน และพาราโบลา

• การหาพื้นที่ของพาราโบลา

ในงานเขียน 24 บทนี้ที่ส่งถึงโดซิเธอุส อาร์คิมิดีสพิสูจน์ด้วยสองวิธีว่าพื้นที่ที่ถูกปิดล้อมด้วยพาราโบลาและเส้นตรงมีค่าเป็น 4/3 เท่าของพื้นที่สามเหลี่ยมที่มีฐานและความสูงเท่ากัน เขาทำได้สำเร็จในหนึ่งในการพิสูจน์โดยการคำนวณค่าของอนุกรมเรขาคณิตที่มีผลรวมเป็นอนันต์ด้วยอัตราส่วน 1/4

• ว่าด้วยทรงกลมและทรงกระบอก

ในตำราสองเล่มนี้ที่ส่งถึงโดซิเธอุส อาร์คิมิดีสได้ผลลัพธ์ที่เขาภาคภูมิใจที่สุด นั่นคือความสัมพันธ์ระหว่างทรงกลมกับทรงกระบอกที่บรรจุอยู่ซึ่งมีความสูงและเส้นผ่านศูนย์กลางเท่ากัน ปริมาตรของทรงกลมคือ 4/3πr³ และสำหรับทรงกระบอกคือ 2πr³ พื้นที่ผิวของทรงกลมคือ 4πr² และสำหรับทรงกระบอกคือ 6πr² (รวมฐานทั้งสองข้าง) โดยที่ r คือรัศมีของทรงกลมและทรงกระบอก

• ว่าด้วยเส้นเกลียว

งานเขียน 28 บทนี้ส่งถึงโดซิเธอุสด้วย ตำรานี้กำหนดสิ่งที่ปัจจุบันเรียกว่าวงก้นหอยของอาร์คิมิดีส มันคือโลกัสของจุดที่สอดคล้องกับตำแหน่งตลอดเวลาของจุดที่เคลื่อนที่ห่างจากจุดคงที่ด้วยความเร็วคงที่ตามแนวเส้นตรงที่หมุนด้วยความเร็วเชิงมุมคงที่ หรือเทียบเท่าในระบบพิกัดเชิงขั้วสมัยใหม่ (r, θ) สามารถอธิบายได้ด้วยสมการ r = a + bθ โดยที่ a และ b เป็นจำนวนจริง นี่เป็นตัวอย่างแรกๆ ของเส้นโค้งเชิงกล (เส้นโค้งที่เกิดจากจุดเคลื่อนที่) ที่นักคณิตศาสตร์กรีกพิจารณา

• ว่าด้วยทรงกรวยและทรงกลม

เป็นงานเขียน 32 บทที่ส่งถึงโดซิเธอุส ในตำรานี้ อาร์คิมิดีสคำนวณพื้นที่และปริมาตรของภาคตัดของกรวย ทรงกลม และพาราโบลอยด์

• ว่าด้วยเทหวัตถุลอย

มีสองเล่มใน On Floating Bodies ในเล่มแรก อาร์คิมิดีสอธิบายกฎของสมดุลของของไหลและพิสูจน์ว่าน้ำจะคงรูปทรงเป็นทรงกลมรอบจุดศูนย์กลางของแรงโน้มถ่วง สิ่งนี้อาจเป็นการพยายามที่จะอธิบายทฤษฎีของนักดาราศาสตร์กรีกร่วมสมัยกับเขา เช่น เอราทอสเทนีส ที่ว่าโลกมีรูปร่างกลม ของไหลที่อาร์คิมิดีสบรรยายนั้นไม่ได้มีแรงโน้มถ่วงในตัวเอง เนื่องจากเขาสมมติฐานว่ามีจุดหนึ่งที่ทุกสิ่งตกลงไปหาเพื่อที่จะได้รูปทรงกลม หลักการของอาร์คิมิดีสว่าด้วยการลอยตัวถูกระบุไว้ในงานเขียนนี้ โดยระบุว่า:
: วัตถุใดๆ ที่จมอยู่ในของไหลไม่ว่าทั้งหมดหรือบางส่วน จะประสบกับแรงต้านที่เท่ากันกับน้ำหนักของของไหลที่ถูกแทนที่ แต่เป็นไปในทิศทางตรงกันข้าม
ในส่วนที่สอง เขาคำนวณตำแหน่งสมดุลของภาคตัดของพาราโบลอยด์ ซึ่งอาจเป็นการสร้างภาพอุดมคติของรูปทรงของท้องเรือ ภาคตัดบางส่วนของเขาลอยโดยมีฐานอยู่ใต้น้ำและยอดอยู่เหนือน้ำ คล้ายกับวิธีที่ภูเขาน้ำแข็งลอย

• โอสโตมาคิออน

หรือที่รู้จักกันในชื่อ Loculus of Archimedes หรือ Archimedes' Box นี่คือปริศนาจำแนกส่วนที่คล้ายคลึงกับแทนแกรม และตำราที่บรรยายถึงมันพบในรูปแบบที่สมบูรณ์ยิ่งขึ้นในสมุดบันทึกของอาร์คิมิดีส อาร์คิมิดีสคำนวณพื้นที่ของชิ้นส่วน 14 ชิ้นที่สามารถประกอบกันเป็นรูปสี่เหลี่ยมจัตุรัส เรวีล เนตซ์ จากมหาวิทยาลัยสแตนฟอร์ดโต้แย้งในปี ค.ศ. 2003 ว่าอาร์คิมิดีสพยายามที่จะกำหนดว่ามีกี่วิธีที่ชิ้นส่วนเหล่านี้สามารถประกอบกันเป็นรูปสี่เหลี่ยมจัตุรัสได้ เนตซ์คำนวณว่าชิ้นส่วนเหล่านี้สามารถประกอบเป็นสี่เหลี่ยมจัตุรัสได้ 17,152 วิธี จำนวนการจัดเรียงคือ 536 เมื่อไม่รวมวิธีแก้ปัญหาที่เทียบเท่ากันโดยการหมุนและการสะท้อน ปริศนานี้เป็นตัวอย่างของปัญหาแรกๆ ในคณิตศาสตร์เชิงการจัด
ที่มาของชื่อปริศนายังไม่ชัดเจน และมีการเสนอว่ามาจากคำภาษากรีกโบราณที่แปลว่า "ลำคอ" หรือ "หลอดอาหาร" คือ stomachos (στόμαχος^{Greek, Ancient}) เอาโซเนียสเรียกปริศนานี้ว่า Ostomachion ซึ่งเป็นคำประสมภาษากรีกที่มาจากรากศัพท์ของ ὀστέον^{Greek, Ancient} (osteon, กระดูก) และ μάχη^{Greek, Ancient} (machē, การต่อสู้)

• ปัญหาเรื่องวัวของอาร์คิมิดีส

ก็อตต์โฮลด์ อีฟราม เลสซิงค้นพบงานนี้ในต้นฉบับภาษากรีกซึ่งประกอบด้วยบทกวี 44 บรรทัดในห้องสมุดเฮอร์ซอก ออกัสต์ในโวลเฟินบึทเทิล ประเทศเยอรมนี ในปี ค.ศ. 1773 งานนี้ส่งถึงเอราทอสเทนีสและนักคณิตศาสตร์ในอเล็กซานเดรีย อาร์คิมิดีสท้าทายพวกเขาให้นับจำนวนวัวในฝูงวัวของเฮลิออสโดยการแก้สมการของไดโอแฟนทัสพร้อมกันหลายสมการ มีปัญหาในเวอร์ชันที่ยากกว่าซึ่งคำตอบบางส่วนต้องเป็นจำนวนกำลังสอง เอ. อัมทอร์เป็นคนแรกที่แก้ปัญหานี้ได้ในปี ค.ศ. 1880 และคำตอบเป็นจำนวนขนาดใหญ่มาก ประมาณ 7.760271 x 10²⁰⁶⁵⁴⁴

• ระเบียบวิธีเกี่ยวกับทฤษฎีบทกลศาสตร์

ตำรานี้เคยถูกคิดว่าสูญหายไปแล้วจนกระทั่งมีการค้นพบสมุดบันทึกของอาร์คิมิดีสในปี ค.ศ. 1906 ในงานเขียนนี้ อาร์คิมิดีสใช้แนวคิดกณิกนันต์ และแสดงให้เห็นว่าการแบ่งรูปทรงออกเป็นส่วนเล็กๆ จำนวนอนันต์สามารถใช้เพื่อกำหนดพื้นที่หรือปริมาตรได้อย่างไร เขาอาจพิจารณาว่าวิธีนี้ขาดความเข้มงวดในเชิงรูปแบบ ดังนั้นเขาจึงใช้ระเบียบวิธีเกษียณเพื่อหาผลลัพธ์ เช่นเดียวกับ ปัญหาเรื่องวัวของอาร์คิมิดีส ระเบียบวิธีเกี่ยวกับทฤษฎีบทกลศาสตร์ เขียนในรูปแบบของจดหมายถึงเอราทอสเทนีสในอเล็กซานเดรีย

5.2. งานที่สูญหาย

ผลงานของอาร์คิมิดีสที่รู้จักกันจากคำอ้างอิงของนักเขียนโบราณอื่นๆ เท่านั้น ได้แก่: On Sphere-Making และงานเกี่ยวกับรูปหลายเหลี่ยมที่กล่าวถึงโดยพัพพัสแห่งอเล็กซานเดรีย; Catoptrica งานเกี่ยวกับแสงที่กล่าวถึงโดยธีออนแห่งอเล็กซานเดรีย; Principles ที่ส่งถึงซีซิพพัสและอธิบายระบบตัวเลขที่ใช้ใน The Sand Reckoner; On Balances หรือ On Levers; On Centers of Gravity; และ On the Calendar

นอกจากนี้ยังมีการกล่าวอ้างว่าสูตรของเฮรอนสำหรับการคำนวณพื้นที่ของสามเหลี่ยมจากความยาวของด้านทั้งสามเป็นที่รู้จักของอาร์คิมิดีส แม้ว่าการปรากฏครั้งแรกของสูตรนี้จะอยู่ในงานของเฮรอนแห่งอเล็กซานเดรียในคริสต์ศตวรรษที่ 1 ผลงานอื่นๆ ที่น่าสงสัยว่าอาร์คิมิดีสเป็นผู้ประพันธ์ ได้แก่ บทกวีละติน Carmen de ponderibus et mensuris (คริสต์ศตวรรษที่ 4 หรือ 5) ซึ่งบรรยายถึงการใช้สมดุลสถิตยศาสตร์ของไหลเพื่อแก้ปัญหามงกุฎ และตำราในคริสต์ศตวรรษที่ 12 ชื่อ Mappae clavicula ซึ่งมีคำแนะนำเกี่ยวกับวิธีการทดสอบโลหะโดยการคำนวณความถ่วงจำเพาะของพวกมัน

5.3. สมุดบันทึกของอาร์คิมิดีส

เอกสารสำคัญที่สุดที่บรรจุผลงานของอาร์คิมิดีสคือสมุดบันทึกของอาร์คิมิดีส ในปี ค.ศ. 1906 ศาสตราจารย์ชาวเดนมาร์กโยฮัน ลุดวิก ไฮเบิร์กได้ไปเยือนคอนสแตนติโนเปิลเพื่อตรวจสอบหนังแพะ 174 หน้าที่เป็นบทสวดมนต์ ซึ่งเขียนขึ้นในคริสต์ศตวรรษที่ 13 หลังจากอ่านคำถอดความสั้นๆ ที่ตีพิมพ์เมื่อเจ็ดปีก่อนโดยปาปาโดปูลอส-เคราเมอุส เขาได้ยืนยันว่ามันเป็นสมุดบันทึกพาลิมเซสต์ ซึ่งเป็นเอกสารที่มีข้อความเขียนทับงานเก่าที่ถูกลบไป การสร้างพาลิมเซสต์ทำได้โดยการขูดหมึกออกจากงานที่มีอยู่แล้วนำกลับมาใช้ใหม่ ซึ่งเป็นวิธีปฏิบัติทั่วไปในยุคกลาง เนื่องจากหนังลูกวัวมีราคาแพง งานเก่าในพาลิมเซสต์ถูกระบุโดยนักวิชาการว่าเป็นสำเนาของตำราที่สูญหายไปแล้วของอาร์คิมิดีสในคริสต์ศตวรรษที่ 10 แผ่นหนังนี้ใช้เวลาหลายร้อยปีในห้องสมุดของอารามในคอนสแตนติโนเปิลก่อนที่จะถูกขายให้กับนักสะสมส่วนตัวในคริสต์ทศวรรษ 1920 เมื่อวันที่ 29 ตุลาคม ค.ศ. 1998 มันถูกขายในการประมูลให้กับผู้ซื้อนิรนามในราคา 2.2 ล้านดอลลาร์

สมุดบันทึกพาลิมเซสต์มีตำราเจ็ดเล่ม รวมถึงสำเนาเดียวที่ยังคงอยู่ของ On Floating Bodies ในภาษากรีกดั้งเดิม มันเป็นแหล่งข้อมูลเดียวที่รู้จักของ The Method of Mechanical Theorems ซึ่งซุยดาสเคยกล่าวถึงและเคยคิดว่าสูญหายไปตลอดกาล Stomachion ก็ถูกค้นพบในพาลิมเซสต์ด้วย โดยมีการวิเคราะห์ปริศนาที่สมบูรณ์กว่าที่เคยพบในข้อความก่อนหน้านี้ สมุดบันทึกพาลิมเซสต์ถูกเก็บไว้ที่พิพิธภัณฑ์ศิลปะวอลเตอร์สในบัลติมอร์ รัฐแมริแลนด์ ซึ่งมีการทดสอบสมัยใหม่หลายอย่าง รวมถึงการใช้แสงอัลตราไวโอเลตและรังสีเอกซ์เพื่ออ่านข้อความที่ถูกเขียนทับลงไป

ตำราในสมุดบันทึกของอาร์คิมิดีสประกอบด้วย:

• ว่าด้วยดุลยภาพของระนาบ
• ว่าด้วยเส้นเกลียว
• ว่าด้วยการวัดวงกลม
• ว่าด้วยทรงกลมและทรงกระบอก
• ว่าด้วยเทหวัตถุลอย
• ระเบียบวิธีเกี่ยวกับทฤษฎีบทกลศาสตร์
• โอสโตมาคิออน
• สุนทรพจน์ของนักการเมืองในคริสต์ศตวรรษที่ 4 ก่อนคริสตกาล ฮิปเปอไรเดส
• คำอธิบายเกี่ยวกับ Categories ของอริสโตเติล
• ผลงานอื่นๆ

6.1. อิทธิพลต่อคณิตศาสตร์และฟิสิกส์

นักประวัติศาสตร์วิทยาศาสตร์และคณิตศาสตร์เกือบทั้งหมดเห็นพ้องต้องกันว่าอาร์คิมิดีสเป็นนักคณิตศาสตร์ที่ยอดเยี่ยมที่สุดในสมัยโบราณ ตัวอย่างเช่น อีริก เทมเพิล เบล เขียนว่า:
"รายชื่อนักคณิตศาสตร์ "ผู้ยิ่งใหญ่" สามคนในประวัติศาสตร์ทั้งหมดจะต้องมีชื่อของอาร์คิมิดีสอยู่ด้วย อีกสองคนมักจะเกี่ยวข้องกับเขาคือไอแซก นิวตันและคาร์ล ฟรีดริช เกาส์ บางคนเมื่อพิจารณาความมั่งคั่ง-หรือความยากจน-ของคณิตศาสตร์และวิทยาศาสตร์กายภาพในยุคที่ยักษ์ใหญ่เหล่านี้มีชีวิตอยู่ และประเมินความสำเร็จของพวกเขาเทียบกับภูมิหลังของยุคสมัยของพวกเขา อาจจะจัดให้อาร์คิมิดีสเป็นอันดับแรก"
ในทำนองเดียวกัน อัลเฟรด นอร์ท ไวต์เฮดและจอร์จ เอฟ. ซิมมอนส์กล่าวถึงอาร์คิมิดีสว่า:
"...ในปี ค.ศ. 1500 ยุโรปรู้จักน้อยกว่าอาร์คิมิดีสผู้เสียชีวิตในปี 212 ปีก่อนคริสตกาล..."
"หากเราพิจารณาสิ่งที่มนุษย์คนอื่นๆ บรรลุผลสำเร็จในคณิตศาสตร์และฟิสิกส์ ในทุกทวีปและทุกอารยธรรม ตั้งแต่เริ่มต้นกาลเวลาจนถึงคริสต์ศตวรรษที่ 17 ในยุโรปตะวันตก ความสำเร็จของอาร์คิมิดีสมีน้ำหนักมากกว่าทั้งหมด เขาเป็นอารยธรรมที่ยิ่งใหญ่ด้วยตัวเขาเอง"
เรวีล เนตซ์ ศาสตราจารย์ด้านคณิตศาสตร์และดาราศาสตร์กรีกที่มหาวิทยาลัยสแตนฟอร์ดและผู้เชี่ยวชาญด้านอาร์คิมิดีสกล่าวว่า:
"ดังนั้น เนื่องจากอาร์คิมิดีสเป็นผู้นำมากกว่าใครๆ ในการก่อตั้งแคลคูลัส และเนื่องจากเขาเป็นผู้บุกเบิกการประยุกต์ใช้คณิตศาสตร์กับโลกทางกายภาพ จึงกลายเป็นว่าวิทยาศาสตร์ตะวันตกเป็นเพียงชุดของเชิงอรรถต่ออาร์คิมิดีส ดังนั้น จึงกลายเป็นว่าอาร์คิมิดีสเป็นนักวิทยาศาสตร์ที่สำคัญที่สุดเท่าที่เคยมีมา"
เลโอนาร์โด ดา วินชีแสดงความชื่นชมต่ออาร์คิมิดีสซ้ำแล้วซ้ำเล่า และยกให้อาร์คิโตเนอร์เป็นสิ่งประดิษฐ์ของอาร์คิมิดีส กาลิเลโอ กาลิเลอีเรียกเขาว่า "เหนือมนุษย์" และ "อาจารย์ของฉัน" ในขณะที่คริสตียาน เฮยเคินส์กล่าวว่า "ฉันคิดว่าอาร์คิมิดีสไม่สามารถเทียบกับใครได้" โดยเลียนแบบเขาอย่างมีสติในผลงานช่วงแรกของเขา กอตต์ฟรีด วิลเฮ็ล์ม ไลบ์นิซกล่าวว่า "ผู้ที่เข้าใจอาร์คิมิดีสและอพอลโลเนียสแห่งเพอร์กาจะชื่นชมความสำเร็จของคนสำคัญในยุคหลังๆ น้อยลง" วีรบุรุษของเกาส์คืออาร์คิมิดีสและนิวตัน และโมริตซ์ คันเตอร์ ผู้ศึกษาภายใต้เกาส์ในมหาวิทยาลัยเกิททิงเงิน รายงานว่าเขาเคยกล่าวในการสนทนาว่า "มีนักคณิตศาสตร์ผู้สร้างยุคเพียงสามคนเท่านั้น: อาร์คิมิดีส, นิวตัน, และกอตต์โฮลด์ ไอเซนสไตน์"
นักประดิษฐ์นิโคลา เทสลายกย่องเขา โดยกล่าวว่า:
"อาร์คิมิดีสคืออุดมคติของฉัน ฉันชื่นชมผลงานของศิลปิน แต่ในความคิดของฉัน พวกมันเป็นเพียงเงาและภาพลวงตา นักประดิษฐ์ต่างหากที่ฉันคิดว่ามอบสิ่งที่จับต้องได้ สิ่งที่มีชีวิตและทำงานได้ให้กับโลก"

6.2. เกียรติยศและการระลึกถึง

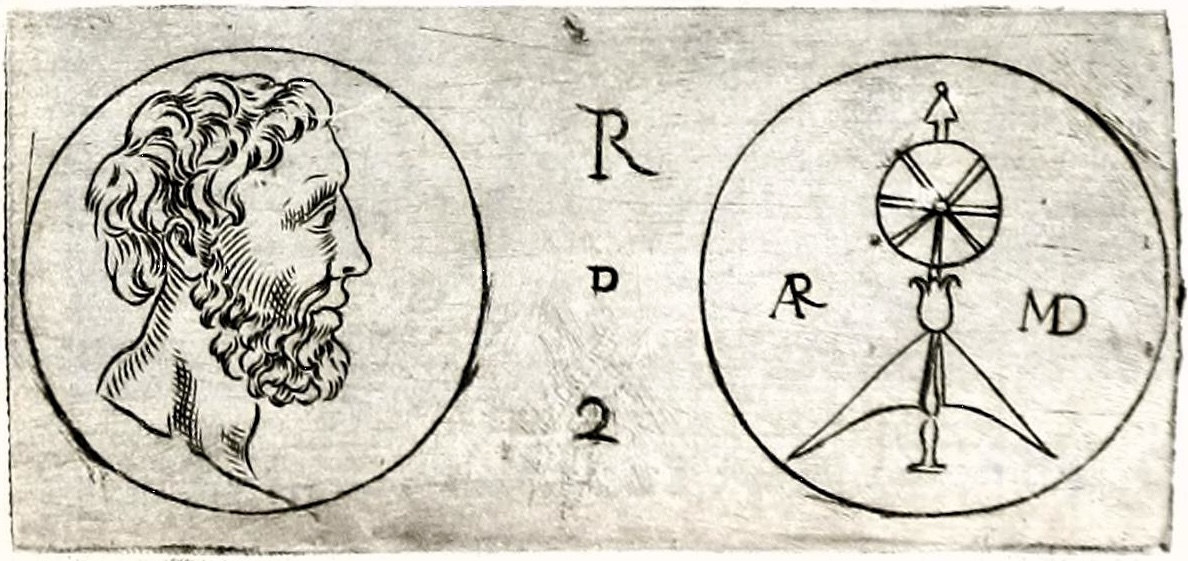
นักเหรียญกษาปณ์และนักโบราณคดีชาวอิตาลี ฟิลิปโป ปารูตา (1552-1629) และ เลโอนาร์โด อาโกสตินี (1593-1676) รายงานเกี่ยวกับเหรียญสำริดในซิซิลีที่มีภาพเหมือนของอาร์คิมิดีสอยู่ด้านหน้า และรูปทรงกระบอกกับทรงกลมพร้อมกับอักษรย่อ ARMD ในภาษาละตินอยู่ด้านหลัง แม้ว่าเหรียญจะสูญหายไปแล้วและไม่ทราบวันที่ผลิตที่แน่นอน อีโว ชไนเดอร์บรรยายด้านหลังว่าเป็น "ทรงกลมที่วางอยู่บนฐาน - อาจเป็นภาพหยาบๆ ของหนึ่งในท้องฟ้าจำลองที่อาร์คิมิดีสสร้างขึ้น" และเสนอว่าอาจถูกผลิตในโรมสำหรับมาร์เซลลัส ผู้ซึ่ง "ตามรายงานโบราณ ได้นำท้องฟ้าจำลองสองลูกของอาร์คิมิดีสมาด้วยที่โรม"

มีหลุมอุกกาบาตบนดวงจันทร์ชื่อหลุมอุกกาบาตอาร์คิมิดีส (29.7, -4.0) เพื่อเป็นเกียรติแก่เขา รวมถึงเทือกเขาบนดวงจันทร์ชื่อมอนเตส อาร์คิมิดีส (25.3, -4.6)

เหรียญฟิลด์สสำหรับความสำเร็จอันโดดเด่นในคณิตศาสตร์มีภาพเหมือนของอาร์คิมิดีส พร้อมกับการแกะสลักที่แสดงการพิสูจน์ของเขาเกี่ยวกับทรงกลมและทรงกระบอก จารึกรอบศีรษะของอาร์คิมิดีสเป็นคำพูดที่มาจากมาร์กุส มานิลลิอุส กวีในคริสต์ศตวรรษที่ 1 ซึ่งเขียนเป็นภาษาละตินว่า: Transire suum pectus mundoque potiri ("จงก้าวข้ามตนเองและเข้าใจโลก")

อาร์คิมิดีสปรากฏบนดวงตราไปรษณียากรที่ออกโดยเยอรมนีตะวันออก (ค.ศ. 1973), กรีซ (ค.ศ. 1983), อิตาลี (ค.ศ. 1983), นิการากัว (ค.ศ. 1971), ซานมารีโน (ค.ศ. 1982) และสเปน (ค.ศ. 1963)
คำอุทาน "ยูเรก้า!" ที่กล่าวอ้างถึงอาร์คิมิดีสเป็นคำขวัญประจำรัฐแคลิฟอร์เนีย ในกรณีนี้ คำนี้หมายถึงการค้นพบทองคำใกล้ซัตเตอร์ส มิลล์ในปี ค.ศ. 1848 ซึ่งจุดประกายยุคตื่นทองแคลิฟอร์เนีย